2.9 KiB
2.9 KiB
Leetcode 01-Matrix
2022-07-17 03:15
Algorithms:
#algorithm #BFS
Data structures:
#DS #vector_2d
Difficulty:
#coding_problem #difficulty-medium
Additional tags:
#leetcode #CS_list_need_understanding
Revisions:
N/A
Related topics:
tag:#BFS
Links:
Problem
Given an m x n binary matrix mat, return the distance of the nearest 0 for each cell.
The distance between two adjacent cells is 1.
Examples
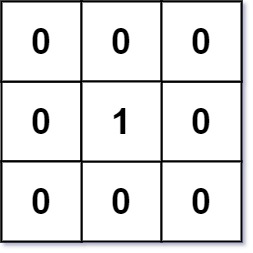
Example 1:
**Input:** mat = [[0,0,0],[0,1,0],[0,0,0]]
**Output:** [[0,0,0],[0,1,0],[0,0,0]]
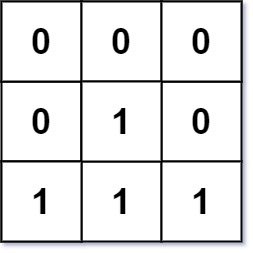
Example 2:
**Input:** mat = [[0,0,0],[0,1,0],[1,1,1]]
**Output:** [[0,0,0],[0,1,0],[1,2,1]]
Constraints
m == mat.lengthn == mat[i].length1 <= m, n <= 1041 <= m * n <= 104mat[i][j]is either0or1.- There is at least one
0inmat.
Thoughts
[!summary] This is a #BFS problem, because it needs to find a smallest distance
Why not DFS
I tried with DFS, but
- it is not suitable for finding smallest distance
- and is easy to go into a infinite loop.
- Also, it is hard to determine whether to revisit (update) the distance.
BFS
Start searching from 0s, because the search direction matters.
pseudo code:
-
Initialization stage:
- add every 0 to queue
- make every 1 a infinite large number, (10001 this case)
-
while queue is not empty
- check for neighbors
- if OOB (Out of Bound), skip
- if the value of neighbor's distance is higher than the node, update it, and add it to queue(also update his neighbors)
- check for neighbors
Solution
class Solution {
const int MAX = 10002;
public:
vector<vector<int>> updateMatrix(vector<vector<int>> &mat) {
// Shouldn't use DFS, since DFS is likely to run into a loop
queue<pair<int, int>> todo;
int m = mat.size(), n = mat[0].size();
for (int i = 0; i < m; i++) {
for (int j = 0; j < n; j++) {
if (mat[i][j] == 0) {
todo.push({i, j});
} else {
mat[i][j] = MAX;
}
}
}
int offset[] = {-1, 1};
int x, y;
int newX, newY;
int dist;
while (!todo.empty()) {
x = todo.front().first;
y = todo.front().second;
todo.pop();
dist = mat[x][y];
for (int i : offset) {
newX = x + i;
if (newX < m && newX >= 0) {
if (mat[newX][y] > dist + 1) {
mat[newX][y] = dist + 1;
todo.push({newX, y});
}
}
newY = y + i;
if (newY < n && newY >= 0) {
if (mat[x][newY] > dist + 1) {
mat[x][newY] = dist + 1;
todo.push({x, newY});
}
}
}
}
return mat;
}
};