notes/OJ notes/pages/Leetcode 01-Matrix.md

# Leetcode 01-Matrix

#### 2022-07-17 03:15

> ##### Algorithms:
> #algorithm #BFS 
> ##### Data structures:
> #DS #vector_2d 
> ##### Difficulty:
> #coding_problem #difficulty-medium 
> ##### Additional tags:
> #leetcode #CS_list_need_understanding 
> ##### Revisions:
> N/A

##### Related topics:
```expander
tag:#BFS
```


##### Links:
- [Link to problem](https://leetcode.com/problems/01-matrix/)
___
### Problem

Given an `m x n` binary matrix `mat`, return _the distance of the nearest_ `0` _for each cell_.

The distance between two adjacent cells is `1`.

#### Examples

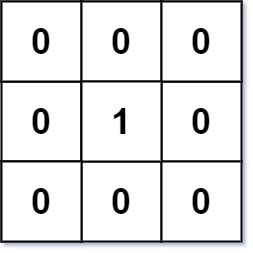
**Example 1:**

![](https://assets.leetcode.com/uploads/2021/04/24/01-1-grid.jpg)

```
**Input:** mat = [[0,0,0],[0,1,0],[0,0,0]]
**Output:** [[0,0,0],[0,1,0],[0,0,0]]
```

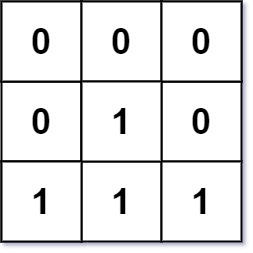
**Example 2:**

![](https://assets.leetcode.com/uploads/2021/04/24/01-2-grid.jpg)

```
**Input:** mat = [[0,0,0],[0,1,0],[1,1,1]]
**Output:** [[0,0,0],[0,1,0],[1,2,1]]
```

#### Constraints

-   `m == mat.length`
-   `n == mat[i].length`
-   `1 <= m, n <= 104`
-   `1 <= m * n <= 104`
-   `mat[i][j]` is either `0` or `1`.
-   There is at least one `0` in `mat`.

### Thoughts

> [!summary]
> This is a #BFS problem, because it needs to find
>  a smallest distance

#### Why not DFS

I tried with DFS, but
1. it is not suitable for finding smallest distance 
2. and is easy to go into a infinite loop.
3. Also, it is hard to determine whether to revisit (update) 
   the distance.

#### BFS

Start searching from 0s, because the search direction matters.

pseudo code:

- Initialization stage:
	- add every 0 to queue
	- make every 1 a infinite large number, (10001 this case)

- while queue is not empty
	- check for neighbors
		- if OOB (Out of Bound), skip
		- if the value of neighbor's distance is higher than 
		  the node, update it, and add it to queue(also update 
		  his neighbors)

### Solution

```cpp
class Solution {
  const int MAX = 10002;

public:
  vector<vector<int>> updateMatrix(vector<vector<int>> &mat) {
    // Shouldn't use DFS, since DFS is likely to run into a loop
    queue<pair<int, int>> todo;
    int m = mat.size(), n = mat[0].size();
    for (int i = 0; i < m; i++) {
      for (int j = 0; j < n; j++) {
        if (mat[i][j] == 0) {
          todo.push({i, j});
        } else {
          mat[i][j] = MAX;
        }
      }
    }

    int offset[] = {-1, 1};
    int x, y;
    int newX, newY;
    int dist;
    while (!todo.empty()) {
      x = todo.front().first;
      y = todo.front().second;
      todo.pop();
      dist = mat[x][y];

      for (int i : offset) {
        newX = x + i;
        if (newX < m && newX >= 0) {
          if (mat[newX][y] > dist + 1) {
            mat[newX][y] = dist + 1;
            todo.push({newX, y});
          }
        }
        newY = y + i;
        if (newY < n && newY >= 0) {
          if (mat[x][newY] > dist + 1) {
            mat[x][newY] = dist + 1;
            todo.push({x, newY});
          }
        }
      }
    }
    return mat;
  }
};
```