109 lines
2.1 KiB
Markdown
109 lines
2.1 KiB
Markdown
# Leetcode Search-a-2D-Matrix
|
|
|
|
#### 2022-06-13 15:33
|
|
|
|
---
|
|
|
|
##### Algorithms:
|
|
|
|
#algorithm #binary_search
|
|
|
|
##### Data structures:
|
|
|
|
#DS #vector #vector_2d
|
|
|
|
##### Difficulty:
|
|
|
|
#leetcode #coding_problem #difficulty-easy
|
|
|
|
##### Related topics:
|
|
|
|
##### Links:
|
|
|
|
- [Link to problem](https://leetcode.com/problems/search-a-2d-matrix/submissions/)
|
|
|
|
---
|
|
|
|
### Problem
|
|
|
|
Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
|
|
|
|
- Integers in each row are sorted from left to right.
|
|
- The first integer of each row is greater than the last integer of the previous row.
|
|
|
|
#### Examples
|
|
|
|
**Example 1:**
|
|
|
|

|
|
|
|
```markdown
|
|
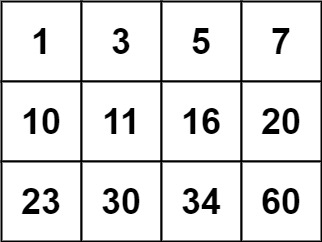
**Input:** matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
|
|
**Output:** true
|
|
```
|
|
|
|
**Example 2:**
|
|
|
|
|
|
|
|
```matrix
|
|
**Input:** matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
|
|
**Output:** false
|
|
```
|
|
|
|
#### Constraints
|
|
|
|
- m == matrix.length
|
|
- n == matrix[i].length
|
|
- 1 <= m, n <= 100
|
|
- -104 <= matrix[i][j], target <= 104
|
|
|
|
### Thoughts
|
|
|
|
Binary search algorithm, with simple 2-d to 1-d conversion
|
|
|
|
> [!tip] Binary search while loops
|
|
> In binary search, remember to check for:
|
|
>
|
|
> - l <= r
|
|
> And use:
|
|
> - l = mid + 1
|
|
> - r = mid - 1
|
|
> Init r as m \* n - 1 to avoid mid being OOB.
|
|
|
|
### Solution
|
|
|
|
==note how I calculated the mid, i, j, and how I changed r and l==
|
|
|
|
```cpp
|
|
class Solution {
|
|
public:
|
|
bool searchMatrix(vector<vector<int>> &matrix, int target) {
|
|
int m = matrix.size();
|
|
int n = matrix[0].size();
|
|
int l = 0;
|
|
// set r to len - 1 to avoid mid being bigger than len.
|
|
int r = m * n - 1;
|
|
int i; // the key to speed is to precaculate i and j, to save time.
|
|
int j;
|
|
int mid;
|
|
|
|
do {
|
|
mid = l + (r - l) / 2;
|
|
i = mid / n;
|
|
j = mid % n;
|
|
if (target == matrix[i][j]) {
|
|
return true;
|
|
} else if (target < matrix[i][j]) {
|
|
r = mid - 1;
|
|
} else {
|
|
l = mid + 1;
|
|
}
|
|
} while (l <= r);
|
|
|
|
return false;
|
|
}
|
|
};
|
|
|
|
```
|