102 lines
2.1 KiB
Markdown
102 lines
2.1 KiB
Markdown
# Leetcode Search-A-2D-Matrix-II
|
|
|
|
2022-09-03 14:57
|
|
|
|
> ##### Algorithms:
|
|
>
|
|
> #algorithm #divide_and_conquer
|
|
>
|
|
> ##### Data structures:
|
|
>
|
|
> #DS #array
|
|
>
|
|
> ##### Difficulty:
|
|
>
|
|
> #coding_problem #difficulty-medium
|
|
>
|
|
> ##### Additional tags:
|
|
>
|
|
> #leetcode #CS_list_need_practicing
|
|
>
|
|
> ##### Revisions:
|
|
>
|
|
> N/A
|
|
|
|
##### Links:
|
|
|
|
- [Link to problem](https://leetcode.com/problems/search-a-2d-matrix-ii/)
|
|
|
|
---
|
|
|
|
### Problem
|
|
|
|
Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
|
|
|
|
- Integers in each row are sorted in ascending from left to right.
|
|
- Integers in each column are sorted in ascending from top to bottom.
|
|
|
|
#### Examples
|
|
|
|
**Example 1:**
|
|
|
|

|
|
|
|
```
|
|
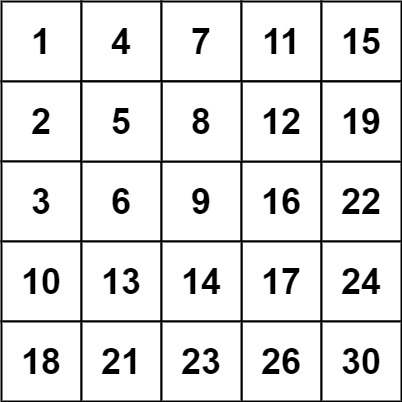
**Input:** matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
|
|
**Output:** true
|
|
```
|
|
|
|
**Example 2:**
|
|
|
|
|
|
|
|
```
|
|
**Input:** matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
|
|
**Output:** false
|
|
```
|
|
|
|
#### Constraints
|
|
|
|
- `m == matrix.length`
|
|
- `n == matrix[i].length`
|
|
- `1 <= n, m <= 300`
|
|
- `-109 <= matrix[i][j] <= 109`
|
|
- All the integers in each row are **sorted** in ascending order.
|
|
- All the integers in each column are **sorted** in ascending order.
|
|
- `-109 <= target <= 109`
|
|
|
|
### Thoughts
|
|
|
|
> [!summary]
|
|
> This is a #divide_and_conquer problem.
|
|
|
|
It's divide and conquer, because every time we do a action,
|
|
the problem is smaller.
|
|
|
|
Start from the top-right, (alternatively, bottom-left),
|
|
because walking left makes the number smaller, and down makes the number bigger.
|
|
|
|
### Solution
|
|
|
|
```cpp
|
|
class Solution {
|
|
public:
|
|
bool searchMatrix(vector<vector<int>> &matrix, int target) {
|
|
// search from top-right
|
|
int c = matrix[0].size() - 1;
|
|
int r = 0;
|
|
int m = matrix.size();
|
|
while (c >= 0 && r < m) {
|
|
if (matrix[r][c] > target) {
|
|
c--;
|
|
} else if (matrix[r][c] < target) {
|
|
r++;
|
|
} else {
|
|
return true;
|
|
}
|
|
}
|
|
|
|
return false;
|
|
}
|
|
};
|
|
``` |