196 lines
5.1 KiB
Markdown
196 lines
5.1 KiB
Markdown
# Floyd's Cycle Finding Algorithm
|
||
|
||
#### 2022-06-14 22:10
|
||
|
||
---
|
||
|
||
##### Algorithms:
|
||
|
||
#algorithm #Floyd_s_cycle_finding_algorithm
|
||
|
||
##### Data structures:
|
||
|
||
#linked_list
|
||
|
||
##### Difficulty:
|
||
|
||
#CS_analysis #difficulty_easy
|
||
|
||
##### Related problems:
|
||
|
||
##### Links:
|
||
|
||
- [g4g](https://www.geeksforgeeks.org/floyds-cycle-finding-algorithm/)
|
||
|
||
---
|
||
|
||
### What is Floyd's Cycle Finding Algorithm?
|
||
|
||
[Floyd’s cycle finding algorithm](https://www.geeksforgeeks.org/detect-loop-in-a-linked-list/) or Hare-Tortoise algorithm is a **pointer algorithm** that uses only **two pointers**, moving through the sequence at different speeds.
|
||
|
||
It uses two pointers one moving twice as fast as the other one. The faster one is called the faster pointer and the other one is called the slow pointer.
|
||
|
||
### How does it work?
|
||
|
||
#### Part 1. **Verify** if there is a loop
|
||
|
||
While traversing the linked list one of these things will occur-
|
||
|
||
- The Fast pointer may reach the end (NULL) this shows that there is no loop n the linked list.
|
||
- The Fast pointer again **catches the slow pointer at some** time therefore a loop exists in the linked list.
|
||
|
||
**Pseudo-code:**
|
||
|
||
- Initialize two-pointers and start traversing the linked list.
|
||
- Move the slow pointer by one position.
|
||
- Move the fast pointer by **two** positions.
|
||
- If both pointers meet at some point then a loop exists and if the fast pointer meets the end position then no loop exists.
|
||
|
||
#### Part 2. **Locating the start** of the loop
|
||
|
||
Let us consider an example:
|
||
|
||
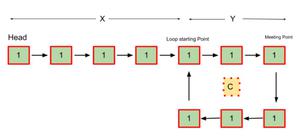
|
||
|
||
- Let,
|
||
|
||
> **X =** Distance between the head(starting) to the loop starting point.
|
||
>
|
||
> **Y =** Distance between the loop starting point and the **first meeting point** of both the pointers.
|
||
>
|
||
> **C =** The distance of **the loop**
|
||
|
||
- So before both the pointer meets-
|
||
|
||
> The slow pointer has traveled **X + Y + s \* C** distance, where s is any positive constant number.
|
||
>
|
||
> The fast pointer has traveled **X + Y + f \* C** distance, where f is any positive constant number.
|
||
|
||
- Since the fast pointer is moving twice as fast as the slow pointer, we can say that the fast pointer covered twice the distance the slow pointer covered. Therefore-
|
||
|
||
> X + Y + f _ C = 2 _ (X + Y + s \* C)
|
||
>
|
||
> X + Y = f _ C – 2 _ s \* C
|
||
>
|
||
> We can say that,
|
||
>
|
||
> f _ C – 2 _ s _ C = (some integer) _ C
|
||
>
|
||
> = K \* C
|
||
>
|
||
> Thus,
|
||
>
|
||
> X + Y = K \* C **– ( 1 )**
|
||
>
|
||
> X = K \* C – Y **– ( 2 )**
|
||
>
|
||
> Where K is some positive constant.
|
||
|
||
- Now if ==reset the slow pointer to the head==(starting position) and move both fast and slow pointer ==by one unit at a time==, one can observe from 1st and 2nd equation that **both of them will meet** after traveling X distance at the starting of the loop because after resetting the slow pointer and moving it X distance, at the same time from loop meeting point the fast pointer will also travel K \* C – Y distance(because it already has traveled Y distance).
|
||
- Because X = K \* C - Y, while fast pointer was at Y from start of loop, running X will place it at the start of loop, meeting the slow pointer.
|
||
|
||
**Pseudo-code**
|
||
|
||
- Place slow pointer at the head.
|
||
- Move one step at a time until they met.
|
||
- The start of the loop is where they met
|
||
|
||
#### Example
|
||
|
||
```cpp
|
||
// C++ program to implement
|
||
// the above approach
|
||
#include <bits/stdc++.h>
|
||
using namespace std;
|
||
|
||
class Node {
|
||
public:
|
||
int data;
|
||
Node *next;
|
||
|
||
Node(int data) {
|
||
this->data = data;
|
||
next = NULL;
|
||
}
|
||
};
|
||
|
||
// initialize a new head
|
||
// for the linked list
|
||
Node *head = NULL;
|
||
class Linkedlist {
|
||
public:
|
||
// insert new value at the start
|
||
void insert(int value) {
|
||
Node *newNode = new Node(value);
|
||
if (head == NULL)
|
||
head = newNode;
|
||
else {
|
||
newNode->next = head;
|
||
head = newNode;
|
||
}
|
||
}
|
||
|
||
// detect if there is a loop
|
||
// in the linked list
|
||
Node *detectLoop() {
|
||
Node *slowPointer = head, *fastPointer = head;
|
||
|
||
while (slowPointer != NULL && fastPointer != NULL &&
|
||
fastPointer->next != NULL) {
|
||
slowPointer = slowPointer->next;
|
||
fastPointer = fastPointer->next->next;
|
||
if (slowPointer == fastPointer)
|
||
break;
|
||
}
|
||
|
||
// if no loop exists
|
||
if (slowPointer != fastPointer)
|
||
return NULL;
|
||
|
||
// reset slow pointer to head
|
||
// and traverse again
|
||
slowPointer = head;
|
||
while (slowPointer != fastPointer) {
|
||
slowPointer = slowPointer->next;
|
||
fastPointer = fastPointer->next;
|
||
}
|
||
|
||
return slowPointer;
|
||
}
|
||
};
|
||
|
||
int main() {
|
||
Linkedlist l1;
|
||
// inserting new values
|
||
l1.insert(10);
|
||
l1.insert(20);
|
||
l1.insert(30);
|
||
l1.insert(40);
|
||
l1.insert(50);
|
||
|
||
// adding a loop for the sake
|
||
// of this example
|
||
Node *temp = head;
|
||
while (temp->next != NULL)
|
||
temp = temp->next;
|
||
// loop added;
|
||
temp->next = head;
|
||
|
||
Node *loopStart = l1.detectLoop();
|
||
if (loopStart == NULL)
|
||
cout << "Loop does not exists" << endl;
|
||
else {
|
||
cout << "Loop does exists and starts from " << loopStart->data << endl;
|
||
}
|
||
|
||
return 0;
|
||
}
|
||
|
||
```
|
||
|
||
### When to use?
|
||
|
||
This algorithm is used ==to find a loop in a linked list==, Also it ==can locate where the loop starts.==
|
||
|
||
It takes O(n) time complexity, O(1)space complexity.
|