EBU6504_smart_arch_notes/4-data-analytics.md

Data analytics: Feature engineering

• Data analytics: Feature engineering
  • Definition
  • Sources of features
  • Feature engineering in ML
    • Types of feature engineering
  • Good feature:
    • Related to objective (important)
    • Known at prediction-time
    • Numeric with meaningful magnitude:
    • Have enough samples
    • Bring human insight to problem
  • Process of Feature Engineering
    • Scaling
      • Rationale:
      • Methods:
        • Normalization or Standardization:
        • Min-max scaling:
        • Robust scaling:
      • Choosing
    • Discretization / Binning / Bucketing
      • Definition
      • Reason for binning
      • Methods
        • Equal width binning
        • Equal frequency binning
        • k means binning
        • decision trees
    • Encoding
    • Transformation
    • Generation

Definition

• The process that attempts to create additional relevant features from existing raw features, to increase the predictive power of algorithms
• Alternative definition: transfer raw data into features that better represent the underlying problem, such that the accuracy of predictive model is improved.
• Important to machine learning

Sources of features

• Different features are needed for different problems, even in the same domain

Feature engineering in ML

• Process of ML iterations:
  • Baseline model -> Feature engineering -> Model 2 -> Feature engineering -> Final
• Example: data needed to predict house price
  • ML can do that with sufficient feature
• Reason for feature engineering: Raw data are rarely useful
  • Must be mapped into a feature vector
  • Good feature engineering takes the most time out of ML

Types of feature engineering

• Indicator variable to isolate information
• Highlighting interactions between features
• Representing the feature in a different way

Good feature:

Related to objective (important)

• Example: the number of concrete blocks around it is not related to house prices

Known at prediction-time

• Some data could be known immediately, and some other data is not known in real time: Can't feed the feature to a model, if it isn't present at prediction time
• Feature definition shouldn't change over time
• Example: If the sales data at prediction time is only available within 3 days, with a 3 day lag, then current sale data can't be used for training (that has to predict with a 3-day old data)

Numeric with meaningful magnitude:

• It does not mean that categorical features can't be used in training: simply, they will need to be transformed through a process called one-hot encoding
• Example: Font category: (Arial, Times New Roman)

Have enough samples

• Have at least five examples of any value before using it in your model
• If features tend to be poorly assorted and are unbalanced, then the trained model will be biased

Bring human insight to problem

• Must have a reason for this feature to be useful, needs subject matter and curious mind
• This is an iterative process, need to use feedback from production usage

Process of Feature Engineering

Scaling

Rationale:

• Leads to a better model, useful when data is uneven: X1 >> X2

Methods:

Normalization or Standardization:

• 𝑍 = \frac{𝑋−𝜇}{\sigma}
• Re-scaled to have a standard normal distribution that centered around 0 with SD of 1
• Will compress the value in the narrow range, if the variable is skewed, or has outliers.
  • This may impair the prediction

Min-max scaling:

• X_{scaled} = \frac{X - min}{max - min}
• Also will compress observation

Robust scaling:

• X_{scaled} = \frac{X - median}{IQR}
• IQR: Interquartile range
• Better at preserving the spread

Choosing

• If data is not guassain like, and has a skewed distribution or outliers : Use robust scaling, as the other two will compress the data to a narrow range, which is not ideal
• For PCA or LDA(distance or covariance calculation), better to use Normalization or Standardization, since it will remove the effect of numerical scale, on variance and covariance
• Min-Max scaling: is bound to 0-1, has same drawback as normalization, and new data may be out of bound (out of original range). This is preferred when the network prefer a 0-1 scale

Discretization / Binning / Bucketing

Definition

• The process of transforming continuous variable into discrete ones, by creating a set of continuous interval, that spans over the range of variable's values
• 

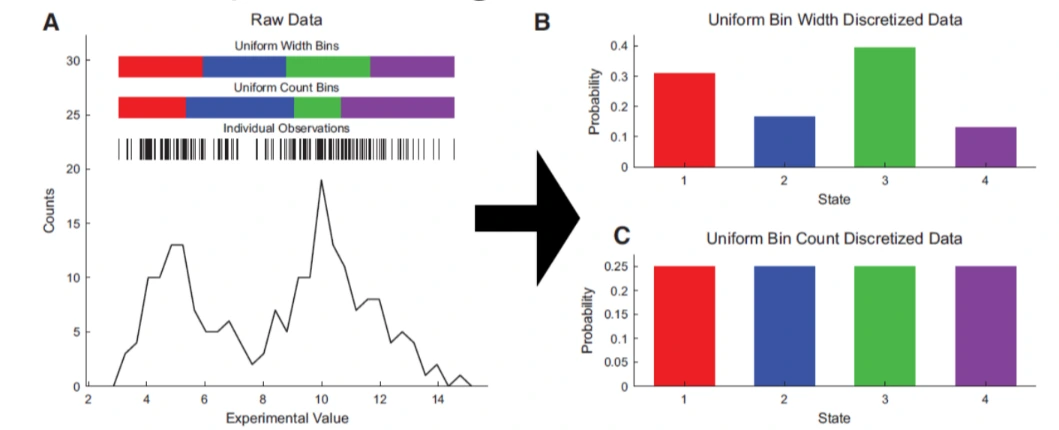
Reason for binning

• Example: Solar energy modeling
  • Acelleration calculation, by binning, and reduce the number of simulation needed
• Improves performance by grouping data with similar attributes and has similar predictive strength
• Improve non-linearity, by being able to capture non-linear patterns , thus improving fitting power of model
• Interpretability is enhanced by grouping
• Reduce the impact of outliers
• Prevent overfitting
• Allow feature interaction, with continuous variables

Methods

Equal width binning

• Divide the scope into bins of the same width
• Con: is sensitive to skewed distribution

Equal frequency binning

• Divides the scope of possible values of variable into N bins, where each bin carries the same number of observations
• Con: May disrupt the relationship with target

k means binning

• Use k-means to partition the values into clusters
• Con: need hyper-parameter tuning

decision trees

• Using decision trees to decide the best splitting points
• Observes which bin is more similar than other bins
• Con:
  • may cause overfitting
  • have a chance of failing: bad performance

Encoding

Transformation

Generation