vault backup: 2022-09-08 16:10:06
This commit is contained in:
parent
45bb95ff62
commit
b128373fa8
2
.obsidian/graph.json
vendored
2
.obsidian/graph.json
vendored
|
|
@ -17,6 +17,6 @@
|
||||||
"repelStrength": 10,
|
"repelStrength": 10,
|
||||||
"linkStrength": 1,
|
"linkStrength": 1,
|
||||||
"linkDistance": 250,
|
"linkDistance": 250,
|
||||||
"scale": 0.3914511147741139,
|
"scale": 0.9583976303921924,
|
||||||
"close": true
|
"close": true
|
||||||
}
|
}
|
||||||
|
|
@ -46,6 +46,9 @@ While traversing the linked list one of these things will occur-
|
||||||
- Move the fast pointer by **two** positions.
|
- Move the fast pointer by **two** positions.
|
||||||
- If both pointers meet at some point then a loop exists and if the fast pointer meets the end position then no loop exists.
|
- If both pointers meet at some point then a loop exists and if the fast pointer meets the end position then no loop exists.
|
||||||
|
|
||||||
|
Example:
|
||||||
|
[[Leetcode Linked-List-Cycle]]
|
||||||
|
|
||||||
#### Part 2. **Locating the start** of the loop
|
#### Part 2. **Locating the start** of the loop
|
||||||
|
|
||||||
Let us consider an example:
|
Let us consider an example:
|
||||||
|
|
@ -95,6 +98,9 @@ Let us consider an example:
|
||||||
- Move one step at a time until they met.
|
- Move one step at a time until they met.
|
||||||
- The start of the loop is where they met
|
- The start of the loop is where they met
|
||||||
|
|
||||||
|
Example:
|
||||||
|
[[Leetcode Linked-List-Cycle-II]]
|
||||||
|
|
||||||
#### Example
|
#### Example
|
||||||
|
|
||||||
```cpp
|
```cpp
|
||||||
|
|
|
||||||
127
OJ notes/pages/Leetcode Linked-List-Cycle-II.md
Normal file
127
OJ notes/pages/Leetcode Linked-List-Cycle-II.md
Normal file
|
|
@ -0,0 +1,127 @@
|
||||||
|
# Leetcode Linked-List-Cycle-II
|
||||||
|
|
||||||
|
2022-09-08 15:56
|
||||||
|
|
||||||
|
> ##### Algorithms:
|
||||||
|
>
|
||||||
|
> #algorithm #Floyd_s_cycle_finding_algorithm
|
||||||
|
>
|
||||||
|
> ##### Data structures:
|
||||||
|
>
|
||||||
|
> #DS #linked_list
|
||||||
|
>
|
||||||
|
> ##### Difficulty:
|
||||||
|
>
|
||||||
|
> #coding_problem #difficulty-medium
|
||||||
|
>
|
||||||
|
> ##### Additional tags:
|
||||||
|
>
|
||||||
|
> #leetcode
|
||||||
|
>
|
||||||
|
> ##### Revisions:
|
||||||
|
>
|
||||||
|
> N/A
|
||||||
|
|
||||||
|
##### Links:
|
||||||
|
|
||||||
|
- [Link to problem](https://leetcode.com/problems/linked-list-cycle-ii/)
|
||||||
|
|
||||||
|
---
|
||||||
|
|
||||||
|
### Problem
|
||||||
|
|
||||||
|
Given the `head` of a linked list, return _the node where the cycle begins. If there is no cycle, return_ `null`.
|
||||||
|
|
||||||
|
There is a cycle in a linked list if there is some node in the list that can be reached again by continuously following the `next` pointer. Internally, `pos` is used to denote the index of the node that tail's `next` pointer is connected to (**0-indexed**). It is `-1` if there is no cycle. **Note that** `pos` **is not passed as a parameter**.
|
||||||
|
|
||||||
|
**Do not modify** the linked list.
|
||||||
|
|
||||||
|
#### Examples
|
||||||
|
|
||||||
|
**Example 1:**
|
||||||
|
|
||||||
|
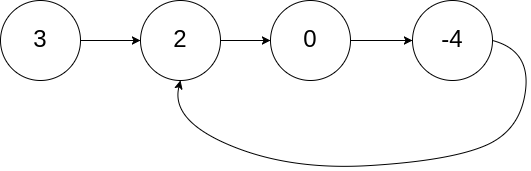
|
||||||
|
|
||||||
|
**Input:** head = [3,2,0,-4], pos = 1
|
||||||
|
**Output:** tail connects to node index 1
|
||||||
|
**Explanation:** There is a cycle in the linked list, where tail connects to the second node.
|
||||||
|
|
||||||
|
**Example 2:**
|
||||||
|
|
||||||
|
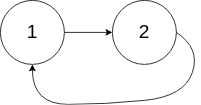
|
||||||
|
|
||||||
|
**Input:** head = [1,2], pos = 0
|
||||||
|
**Output:** tail connects to node index 0
|
||||||
|
**Explanation:** There is a cycle in the linked list, where tail connects to the first node.
|
||||||
|
|
||||||
|
**Example 3:**
|
||||||
|
|
||||||
|

|
||||||
|
|
||||||
|
**Input:** head = [1], pos = -1
|
||||||
|
**Output:** no cycle
|
||||||
|
**Explanation:** There is no cycle in the linked list.
|
||||||
|
|
||||||
|
#### Constraints
|
||||||
|
|
||||||
|
- The number of the nodes in the list is in the range `[0, 104]`.
|
||||||
|
- `-105 <= Node.val <= 105`
|
||||||
|
- `pos` is `-1` or a **valid index** in the linked-list.
|
||||||
|
|
||||||
|
### Thoughts
|
||||||
|
|
||||||
|
> [!summary]
|
||||||
|
> This is a #Floyd_s_cycle_finding_algorithm phase 2
|
||||||
|
> problem.
|
||||||
|
|
||||||
|
Already explained in [[Floyd's Cycle Finding Algorithm]]
|
||||||
|
|
||||||
|
A follow-up to [[Leetcode Linked-List-Cycle]]
|
||||||
|
|
||||||
|
One thing to remember is that in the beginning,
|
||||||
|
fast == slow, which makes the while loop break.
|
||||||
|
|
||||||
|
### Solution
|
||||||
|
|
||||||
|
```cpp
|
||||||
|
/**
|
||||||
|
* Definition for singly-linked list.
|
||||||
|
* struct ListNode {
|
||||||
|
* int val;
|
||||||
|
* ListNode *next;
|
||||||
|
* ListNode(int x) : val(x), next(NULL) {}
|
||||||
|
* };
|
||||||
|
*/
|
||||||
|
class Solution {
|
||||||
|
public:
|
||||||
|
ListNode *detectCycle(ListNode *head) {
|
||||||
|
// Floyed's circle finding algorithm
|
||||||
|
|
||||||
|
ListNode *fast = head;
|
||||||
|
ListNode *slow = head;
|
||||||
|
bool hasLoop = false;
|
||||||
|
|
||||||
|
while (fast != nullptr && fast->next != nullptr) {
|
||||||
|
fast = fast->next->next;
|
||||||
|
slow = slow->next;
|
||||||
|
if (fast && fast == slow) {
|
||||||
|
// loop found
|
||||||
|
hasLoop = true;
|
||||||
|
break;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
|
||||||
|
if (hasLoop == false) {
|
||||||
|
return nullptr;
|
||||||
|
} else {
|
||||||
|
slow = head;
|
||||||
|
while (slow != fast) {
|
||||||
|
slow = slow->next;
|
||||||
|
fast = fast->next;
|
||||||
|
}
|
||||||
|
|
||||||
|
return slow;
|
||||||
|
}
|
||||||
|
}
|
||||||
|
};
|
||||||
|
```
|
||||||
|
|
@ -61,6 +61,8 @@ In **Pascal's triangle**, each number is the sum of the two numbers directly abo
|
||||||
|
|
||||||
> [!summary]
|
> [!summary]
|
||||||
> This is a #recursion problem.
|
> This is a #recursion problem.
|
||||||
|
>
|
||||||
|
> Follow up of [[Leetcode Pascal's-Triangle]]
|
||||||
|
|
||||||
Because to get the nth row, we have to get the `n - 1` th
|
Because to get the nth row, we have to get the `n - 1` th
|
||||||
row, we use recursion.
|
row, we use recursion.
|
||||||
|
|
|
||||||
Loading…
Reference in a new issue