vault backup: 2022-09-03 15:06:04
This commit is contained in:
parent
5b0022c21a
commit
4c3b8a0335
2
.obsidian/appearance.json
vendored
2
.obsidian/appearance.json
vendored
|
|
@ -1,5 +1,5 @@
|
|||
{
|
||||
"theme": "moonstone",
|
||||
"theme": "obsidian",
|
||||
"translucency": true,
|
||||
"cssTheme": "Atom",
|
||||
"interfaceFontFamily": "IBM Plex Sans",
|
||||
|
|
|
|||
8
.obsidian/graph.json
vendored
8
.obsidian/graph.json
vendored
|
|
@ -1,9 +1,9 @@
|
|||
{
|
||||
"collapse-filter": false,
|
||||
"search": "",
|
||||
"showTags": false,
|
||||
"showTags": true,
|
||||
"showAttachments": false,
|
||||
"hideUnresolved": false,
|
||||
"hideUnresolved": true,
|
||||
"showOrphans": false,
|
||||
"collapse-color-groups": false,
|
||||
"colorGroups": [
|
||||
|
|
@ -32,6 +32,6 @@
|
|||
"repelStrength": 10,
|
||||
"linkStrength": 1,
|
||||
"linkDistance": 250,
|
||||
"scale": 0.6816823949098497,
|
||||
"close": true
|
||||
"scale": 0.8153718570546561,
|
||||
"close": false
|
||||
}
|
||||
59
OJ notes/pages/Leetcode Search-A-2D-Matrix-II.md
Normal file
59
OJ notes/pages/Leetcode Search-A-2D-Matrix-II.md
Normal file
|
|
@ -0,0 +1,59 @@
|
|||
# Leetcode Search-A-2D-Matrix-II
|
||||
|
||||
2022-09-03 14:57
|
||||
|
||||
> ##### Algorithms:
|
||||
> #algorithm #divide_and_conquer
|
||||
> ##### Data structures:
|
||||
> #DS #array
|
||||
> ##### Difficulty:
|
||||
> #coding_problem #difficulty-medium
|
||||
> ##### Additional tags:
|
||||
> #leetcode
|
||||
> ##### Revisions:
|
||||
> N/A
|
||||
|
||||
##### Links:
|
||||
- [Link to problem](https://leetcode.com/problems/search-a-2d-matrix-ii/)
|
||||
___
|
||||
### Problem
|
||||
|
||||
Write an efficient algorithm that searches for a value `target` in an `m x n` integer matrix `matrix`. This matrix has the following properties:
|
||||
|
||||
- Integers in each row are sorted in ascending from left to right.
|
||||
- Integers in each column are sorted in ascending from top to bottom.
|
||||
|
||||
#### Examples
|
||||
|
||||
**Example 1:**
|
||||
|
||||

|
||||
|
||||
```
|
||||
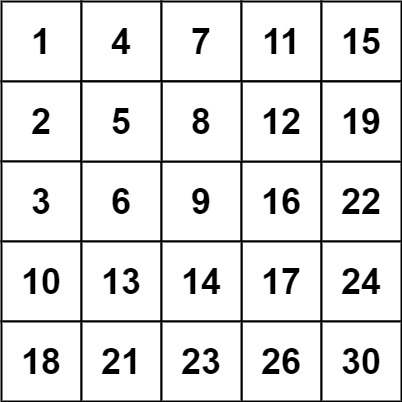
**Input:** matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
|
||||
**Output:** true
|
||||
```
|
||||
|
||||
**Example 2:**
|
||||
|
||||
|
||||
|
||||
```
|
||||
**Input:** matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
|
||||
**Output:** false
|
||||
```
|
||||
|
||||
#### Constraints
|
||||
|
||||
### Thoughts
|
||||
|
||||
> [!summary]
|
||||
> This is a #divide_and_conquer problem.
|
||||
|
||||
It's divide and conquer, because every time we do a action,
|
||||
the problem is smaller.
|
||||
|
||||
Start from the top-right, (alternatively, bottom-left),
|
||||
because walking left makes the number smaller, and down makes the number bigger.
|
||||
|
||||
### Solution
|
||||
Loading…
Reference in a new issue