vault backup: 2022-07-15 10:12:32

OJ notes/pages/Leetcode Max-Area-of-Island.md

@@ -0,0 +1,206 @@
+# Leetcode Max-Area-of-Island
+
+#### 2022-07-15 10:00
+
+> ##### Algorithms:
+> #algorithm 
+> ##### Data structures:
+> #DS #vector_2d 
+> ##### Difficulty:
+> #coding_problem #difficulty-medium 
+> ##### Additional tags:
+> #leetcode 
+> ##### Revisions:
+> N/A
+
+##### Related topics:
+```expander
+tag:#BFS OF tag:#DFS
+```
+ 
+ 
+
+##### Links:
+- [Link to problem](https://leetcode.com/problems/max-area-of-island/)
+___
+### Problem
+
+You are given an `m x n` binary matrix `grid`. An island is a group of `1`'s (representing land) connected **4-directionally** (horizontal or vertical.) You may assume all four edges of the grid are surrounded by water.
+
+The **area** of an island is the number of cells with a value `1` in the island.
+
+Return _the maximum **area** of an island in_ `grid`. If there is no island, return `0`.
+
+#### Examples
+
+**Example 1:**
+
+![](https://assets.leetcode.com/uploads/2021/05/01/maxarea1-grid.jpg)
+
+```
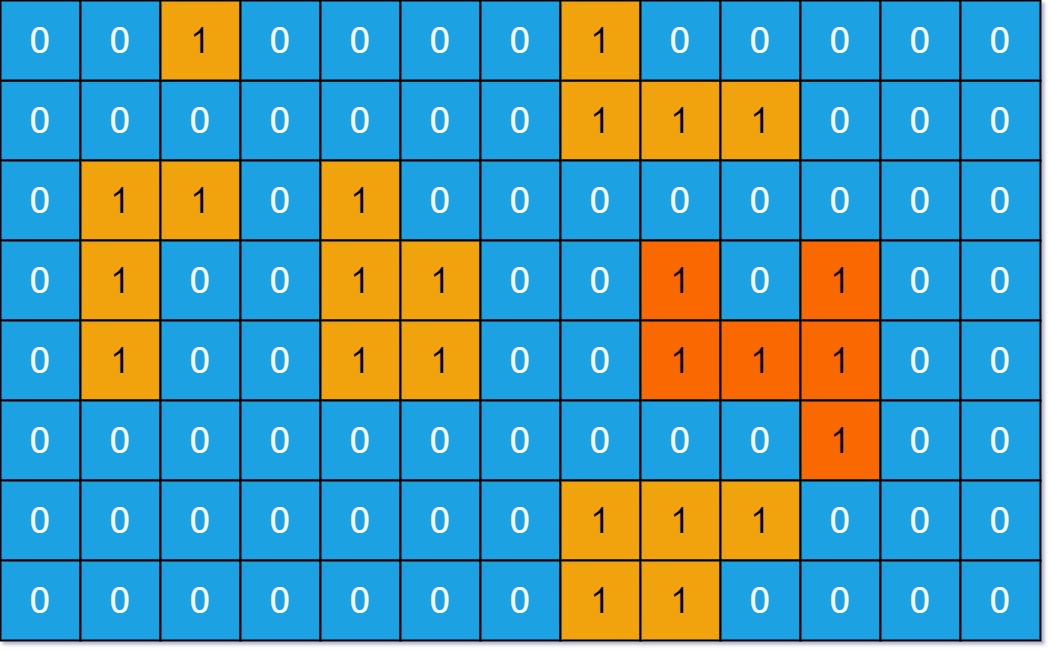
+**Input:** grid = [[0,0,1,0,0,0,0,1,0,0,0,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,1,1,0,1,0,0,0,0,0,0,0,0],[0,1,0,0,1,1,0,0,1,0,1,0,0],[0,1,0,0,1,1,0,0,1,1,1,0,0],[0,0,0,0,0,0,0,0,0,0,1,0,0],[0,0,0,0,0,0,0,1,1,1,0,0,0],[0,0,0,0,0,0,0,1,1,0,0,0,0]]
+**Output:** 6
+**Explanation:** The answer is not 11, because the island must be connected 4-directionally.
+```
+
+**Example 2:**
+
+```
+**Input:** grid = [[0,0,0,0,0,0,0,0]]
+**Output:** 0
+```
+
+#### Constraints
+
+-   `m == grid.length`
+-   `n == grid[i].length`
+-   `1 <= m, n <= 50`
+-   `grid[i][j]` is either `0` or `1`.
+
+### Thoughts
+
+> [!summary]
+> This is a search problem, can be implemented using #DFS or #BFS 
+
+Simple O(mn) solution.
+
+We keep track of pile we visited, using:
+- an 2-d bool vector visited(which is the one I'm using)
+- change the value of pile to 0
+
+And for each unvisited pile, run DFS or BFS to check the size, and keep track of max size with a variable
+
+### Solution
+
+BFS
+```cpp
+class Solution {
+  int getSize(vector<vector<int>> &grid, int m, int n, int x, int y,
+              vector<vector<bool>> &visited) {
+    queue<pair<int, int>> todo;
+    todo.push({x, y});
+    int r, c;
+    int size = 0;
+
+    while (!todo.empty()) {
+      r = todo.front().first;
+      c = todo.front().second;
+      todo.pop();
+
+      if (visited[r][c] || grid[r][c] != 1) {
+        // Visited this place, or the color is not 1
+        continue;
+      }
+
+      size++;
+      visited[r][c] = true;
+
+      if (r > 0) {
+        todo.push({r - 1, c});
+      }
+      if (r < m - 1) {
+        todo.push({r + 1, c});
+      }
+      if (c > 0) {
+        todo.push({r, c - 1});
+      }
+      if (c < n - 1) {
+        todo.push({r, c + 1});
+      }
+    }
+
+    return size;
+  }
+
+public:
+  int maxAreaOfIsland(vector<vector<int>> &grid) {
+    int m = grid.size(), n = grid[0].size();
+    int maxSize = 0;
+
+    vector<vector<bool>> visited;
+    for (int i = 0; i < m; i++) {
+      visited.push_back({});
+      for (int j = 0; j < n; j++) {
+        visited.back().push_back(false);
+      }
+    }
+
+    for (int i = 0; i < m; i++) {
+      for (int j = 0; j < n; j++) {
+        if (grid[i][j] == 1 && !visited[i][j]) {
+          maxSize = max(maxSize, getSize(grid, m, n, i, j, visited));
+        }
+      }
+    }
+    return maxSize;
+  }
+};
+```
+
+DFS iterative (simply change from queue to stack in BFS)
+```cpp
+class Solution {
+  // DFS iterative
+  int getSize(vector<vector<int>> &grid, int m, int n, int x, int y,
+              vector<vector<bool>> &visited) {
+    stack<pair<int, int>> todo;
+    todo.push({x, y});
+    int r, c;
+    int size = 0;
+
+    while (!todo.empty()) {
+      r = todo.top().first;
+      c = todo.top().second;
+      todo.pop();
+
+      if (visited[r][c] || grid[r][c] != 1) {
+        // Visited this place, or the color is not 1
+        continue;
+      }
+
+      size++;
+      visited[r][c] = true;
+
+      if (r > 0) {
+        todo.push({r - 1, c});
+      }
+      if (r < m - 1) {
+        todo.push({r + 1, c});
+      }
+      if (c > 0) {
+        todo.push({r, c - 1});
+      }
+      if (c < n - 1) {
+        todo.push({r, c + 1});
+      }
+    }
+
+    return size;
+  }
+
+public:
+  int maxAreaOfIsland(vector<vector<int>> &grid) {
+    int m = grid.size(), n = grid[0].size();
+    int maxSize = 0;
+
+    vector<vector<bool>> visited;
+    for (int i = 0; i < m; i++) {
+      visited.push_back({});
+      for (int j = 0; j < n; j++) {
+        visited.back().push_back(false);
+      }
+    }
+
+    for (int i = 0; i < m; i++) {
+      for (int j = 0; j < n; j++) {
+        if (grid[i][j] == 1 && !visited[i][j]) {
+          maxSize = max(maxSize, getSize(grid, m, n, i, j, visited));
+        }
+      }
+    }
+    return maxSize;
+  }
+};
+```
+
+DFS recursive