98 lines
2.6 KiB
Markdown
98 lines
2.6 KiB
Markdown
|
|
# Leetcode Lowest-Common-Ancestor-Of-a-Binary-Search-Tree
|
||
|
|
|
||
|
|
#### 2022-07-08 11:53
|
||
|
|
|
||
|
|
> ##### Algorithms:
|
||
|
|
> #algorithm #binary_search #DFS
|
||
|
|
> ##### Data structures:
|
||
|
|
> #DS #binary_tree #binary_search_tree
|
||
|
|
> ##### Difficulty:
|
||
|
|
> #coding_problem #difficulty-easy
|
||
|
|
> ##### Additional tags:
|
||
|
|
> #leetcode
|
||
|
|
> ##### Revisions:
|
||
|
|
> N/A
|
||
|
|
|
||
|
|
##### Related topics:
|
||
|
|
##### Links:
|
||
|
|
- [Link to problem](https://leetcode.com/problems/lowest-common-ancestor-of-a-binary-search-tree/)
|
||
|
|
___
|
||
|
|
### Problem
|
||
|
|
|
||
|
|
Given a binary search tree (BST), find the lowest common ancestor (LCA) of two given nodes in the BST.
|
||
|
|
|
||
|
|
According to the [definition of LCA on Wikipedia](https://en.wikipedia.org/wiki/Lowest_common_ancestor): “The lowest common ancestor is defined between two nodes `p` and `q` as the lowest node in `T` that has both `p` and `q` as descendants (where we allow **a node to be a descendant of itself**).”
|
||
|
|
|
||
|
|
#### Examples
|
||
|
|
|
||
|
|
**Example 1:**
|
||
|
|
|
||
|
|
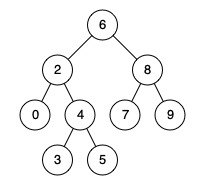
|
||
|
|
|
||
|
|
**Input:** root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 8
|
||
|
|
**Output:** 6
|
||
|
|
**Explanation:** The LCA of nodes 2 and 8 is 6.
|
||
|
|
|
||
|
|
**Example 2:**
|
||
|
|
|
||
|
|

|
||
|
|
|
||
|
|
**Input:** root = [6,2,8,0,4,7,9,null,null,3,5], p = 2, q = 4
|
||
|
|
**Output:** 2
|
||
|
|
**Explanation:** The LCA of nodes 2 and 4 is 2, since a node can be a descendant of itself according to the LCA definition.
|
||
|
|
|
||
|
|
**Example 3:**
|
||
|
|
|
||
|
|
**Input:** root = [2,1], p = 2, q = 1
|
||
|
|
**Output:** 2
|
||
|
|
|
||
|
|
#### Constraints
|
||
|
|
|
||
|
|
- The number of nodes in the tree is in the range `[2, 105]`.
|
||
|
|
- `-109 <= Node.val <= 109`
|
||
|
|
- All `Node.val` are **unique**.
|
||
|
|
- `p != q`
|
||
|
|
- `p` and `q` will exist in the BST.
|
||
|
|
|
||
|
|
### Thoughts
|
||
|
|
|
||
|
|
> [!summary]
|
||
|
|
> This is a #binary_search
|
||
|
|
|
||
|
|
Because of the features of BST, the maximum val of a left sub-tree is smaller than node, so the valid LCA must meet this:
|
||
|
|
```
|
||
|
|
root->val >= small && root->val <= big
|
||
|
|
```
|
||
|
|
otherwise, search the left or right subtree.
|
||
|
|
|
||
|
|
### Solution
|
||
|
|
|
||
|
|
```cpp
|
||
|
|
/**
|
||
|
|
* Definition for a binary tree node.
|
||
|
|
* struct TreeNode {
|
||
|
|
* int val;
|
||
|
|
* TreeNode *left;
|
||
|
|
* TreeNode *right;
|
||
|
|
* TreeNode(int x) : val(x), left(NULL), right(NULL) {}
|
||
|
|
* };
|
||
|
|
*/
|
||
|
|
|
||
|
|
class Solution {
|
||
|
|
public:
|
||
|
|
TreeNode* lowestCommonAncestor(TreeNode* root, TreeNode* p, TreeNode* q) {
|
||
|
|
// DFS-like recursion
|
||
|
|
// Base cases
|
||
|
|
int big = max(q->val, p->val);
|
||
|
|
int small = min(q->val, p->val);
|
||
|
|
|
||
|
|
if (root->val >= small && root->val <= big) {
|
||
|
|
return root;
|
||
|
|
} else if (root->val > big) {
|
||
|
|
return lowestCommonAncestor(root->left, p, q);
|
||
|
|
} else {
|
||
|
|
return lowestCommonAncestor(root->right, p, q);
|
||
|
|
}
|
||
|
|
}
|
||
|
|
};
|
||
|
|
```
|