96 lines
2.4 KiB
Markdown
96 lines
2.4 KiB
Markdown
|
|
# Leetcode Insert-Into-a-Binary-Search-Tree
|
|||
|
|
|
|||
|
|
#### 2022-07-07 08:50
|
|||
|
|
|
|||
|
|
> ##### Algorithms:
|
|||
|
|
> #algorithm #recursion #DFS
|
|||
|
|
> ##### Data structures:
|
|||
|
|
> #DS #binary_tree
|
|||
|
|
> ##### Difficulty:
|
|||
|
|
> #coding_problem #difficulty-medium
|
|||
|
|
> ##### Additional tags:
|
|||
|
|
> #leetcode
|
|||
|
|
> ##### Revisions:
|
|||
|
|
> N/A
|
|||
|
|
|
|||
|
|
##### Related topics:
|
|||
|
|
```expander
|
|||
|
|
tag:#DFS
|
|||
|
|
```
|
|||
|
|
|
|||
|
|
- [[Leetcode Binary-Tree-Inorder-Traversal]]
|
|||
|
|
- [[Leetcode Binary-Tree-Postorder-Traversal]]
|
|||
|
|
- [[Leetcode Binary-Tree-Preorder-Traversal]]
|
|||
|
|
- [[Leetcode Invert-Binary-Tree]]
|
|||
|
|
- [[Leetcode Maximum-Depth-Of-Binary-Tree]]
|
|||
|
|
- [[Leetcode Path-Sum]]
|
|||
|
|
- [[Leetcode Search-In-a-Binary-Tree]]
|
|||
|
|
- [[Leetcode Symmetric-Tree]]
|
|||
|
|
|
|||
|
|
|
|||
|
|
##### Links:
|
|||
|
|
- [Link to problem](https://leetcode.com/problems/insert-into-a-binary-search-tree/)
|
|||
|
|
___
|
|||
|
|
### Problem
|
|||
|
|
|
|||
|
|
You are given the root node of a binary search tree (BST) and a value to insert into the tree. Return the root node of the BST after the insertion. It is guaranteed that the new value does not exist in the original BST.
|
|||
|
|
|
|||
|
|
Notice that there may exist multiple valid ways for the insertion, as long as the tree remains a BST after insertion. You can return any of them.
|
|||
|
|
|
|||
|
|
#### Examples
|
|||
|
|
|
|||
|
|
**Example 1:**
|
|||
|
|
|
|||
|
|

|
|||
|
|
|
|||
|
|
**Input:** root = [4,2,7,1,3], val = 5
|
|||
|
|
**Output:** [4,2,7,1,3,5]
|
|||
|
|
**Explanation:** Another accepted tree is:
|
|||
|
|
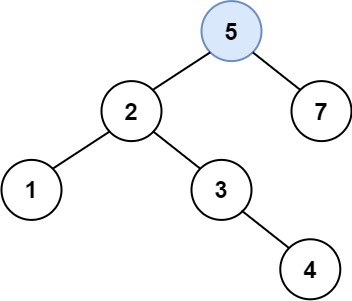
|
|||
|
|
|
|||
|
|
**Example 2:**
|
|||
|
|
|
|||
|
|
**Input:** root = [40,20,60,10,30,50,70], val = 25
|
|||
|
|
**Output:** [40,20,60,10,30,50,70,null,null,25]
|
|||
|
|
|
|||
|
|
**Example 3:**
|
|||
|
|
|
|||
|
|
**Input:** root = [4,2,7,1,3,null,null,null,null,null,null], val = 5
|
|||
|
|
**Output:** [4,2,7,1,3,5]
|
|||
|
|
|
|||
|
|
#### Constraints
|
|||
|
|
|
|||
|
|
- The number of nodes in the tree will be in the range `[0, 104]`.
|
|||
|
|
- `-108 <= Node.val <= 108`
|
|||
|
|
- All the values `Node.val` are **unique**.
|
|||
|
|
- `-108 <= val <= 108`
|
|||
|
|
- It's **guaranteed** that `val` does not exist in the original BST.
|
|||
|
|
|
|||
|
|
### Thoughts
|
|||
|
|
|
|||
|
|
> [!summary]
|
|||
|
|
> This is a #DFS problem.
|
|||
|
|
|
|||
|
|
Seems that no one seems to care about the second way, since it's way too complex.
|
|||
|
|
|
|||
|
|
#### DFS
|
|||
|
|
|
|||
|
|
DFS-like solution is a simple recursion problem, using a helper function.
|
|||
|
|
|
|||
|
|
##### Edge case:
|
|||
|
|
|
|||
|
|
root is null, simple return a new node.
|
|||
|
|
|
|||
|
|
##### Base cases:
|
|||
|
|
- left side is empty, and val < root->val: place it in
|
|||
|
|
- right side is empty, and val > root->val: place it in
|
|||
|
|
|
|||
|
|
##### Pseudocode:
|
|||
|
|
- check for base cases
|
|||
|
|
- if val < root->val, insert(root->left, val)
|
|||
|
|
- vice, versa.
|
|||
|
|
|
|||
|
|
#### BFS
|
|||
|
|
|
|||
|
|
### Solution
|